拉伸彈簧作為工業生產系統當中的一個主要零件,它有著非常大的使用量,而且拉伸彈簧的種類非常的繁多復雜,所以拉伸彈簧的制造由原始的手工制造漸漸地走向自動化生產。
如今,我們所使用的拉伸彈簧應力與變形的計算公式都是依據材料的力學所推導出來的,隨著時代和設計應力的進步,像以前很多的經驗都已經不再適用了。所以,我們一定要使用精密的解析技術,現在應用比較廣泛的方法也就是有限元法。
近些年來,拉伸彈簧的有限元法開始逐漸進入了適用階段,呈現了很多有用的價值數據。對于兩個相同構造的拉伸彈簧,在相同情況的作用力下,有效圈少的或螺旋角大的風吹草動應力彈簧的應力,兩種方法得出的結果差別比較大。這是由于隨著螺旋角的增大,加之載荷偏心,使拉伸彈簧外徑或橫向變形較大,因而應力也較大。用現行的設計計算方法不能確切地反映,而有限元規律以較為確切地反映出來。
圓柱螺旋拉伸彈簧受壓或受拉時,彈簧絲的受力情況是完全一樣的。圓形截面彈簧絲的拉伸彈簧承受軸向載荷,由于彈簧絲具有升角α,故在通過彈簧軸線的截面上,彈簧絲的截面呈橢圓形,該截面上作用著力及扭矩 。 因而在彈簧絲的法向截面上則作用有橫向力、軸向力、彎矩及扭矩。 由于彈簧的螺旋升角一般取為α=5°~9°,故sinα≈0;cosα≈1。為了使彈簧本身較為穩定,不致顫動和過軟,C值不能太大;但為避免卷繞時彈簧絲受到強烈彎曲,C值又不應太小。C值的范圍為4~16, 常用值為5~8。常用旋繞比C值:d(mm) 0.2~0.4 0.45~1 1.1~2.2 2.5~6 7~16 18~42 C=D2/d 7~14 5~12 5~10 4~9 4~8 4~6,為了簡化計算,通常在上式中取1+2C≈2C(因為當C=4~16時,2C>>l,實質上即為略去了),由于彈簧絲升角和曲率的影響,彈簧絲截面中的應力分布將最大應力產生在彈簧絲截面內側的m點。實踐證明,拉伸彈簧的破壞也大多由這點開始。為了考慮彈簧絲的升角和曲率對彈簧絲中應力的影響。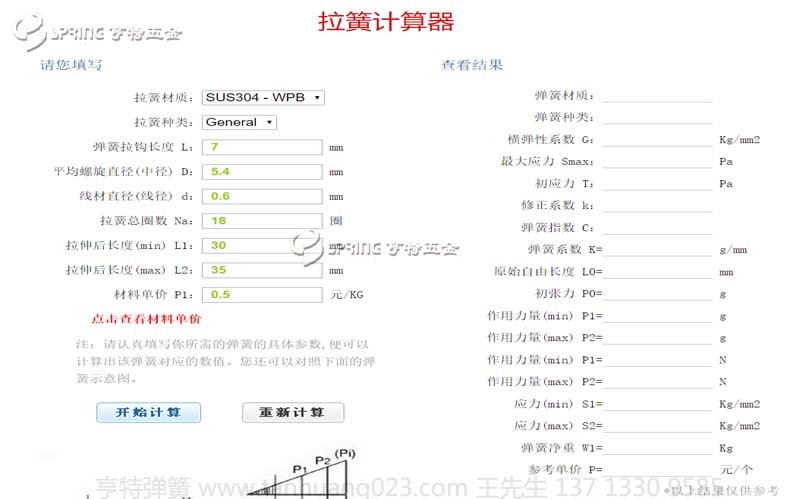
本站提供在線拉伸彈簧計算軟件,軟件提供拉伸彈簧設計常規數據,為前期產品設計提供有力的技術支撐。本軟件計算數據為理論數據,產品設計中須留有一定余量。本軟件除計算拉伸彈簧性能外還支持彈簧的成本計算,含拉伸彈簧自重及市場成本,為企業采購提供一定的預算。


